 Risk 風險 Risk 風險
很多人對風險這個字存有很嚴重的誤解。
在許多的眼中,風險常常只看其「負面」,而沒有看其「正面」。
實際收入比預期收入高,是好事,被視為「利」。
實際收入比預期收入低,是壞事,被視為「風險」。
其實以上兩種皆是風險,不管好與壞,有偏差就是風險。
風險,以現今通用的定義,是指「預期的偏差」。
預期,如預期收入,結果與預期不同,就是偏差了。
|
風險
對將來收入的不確定( Uncertainly )﹔
預期收入的偏差( Variance )
|
這偏差沒有好壞之分。實際收入有 10%,而預期收入是 8%,結果比預期的好,也許是好事吧,
至少許多人也這樣認為,但這「不同」,即是偏差,亦是風險。
我一位十分敬重的老師李博士,他將風險看成「波動」。波動很大,時高時低,不容易捉緊。
我本人很喜歡這個看法。以波動大,來形容風險高,十分貼切。然而這也是現今主流的看法。
在當今的財務學中,風險以統計學中標準差( Standard Deviation )或方差( Variance )量度及表示。
給大家一個例子吧。現在有一件資產,在過去 5 年的回報率如下﹕
| 年 |
1 |
2 |
3 |
4 |
5 |
| 回報率 |
10% |
8% |
9% |
12% |
7% |
首先,找出這一列數字的平均數。( 10% + 8% + 9% + 12% + 7% ) / 5 = 9.2%
其次,找出每一個回報率與這個平均回報率的差距,「相減」是也。( 每一個回報率 - 平均回報率 )
| 年 |
1 |
2 |
3 |
4 |
5 |
Total |
| 相差 |
0.8% |
- 1.2% |
- 0.2% |
2.8% |
- 2.2% |
0 |
把這些差額自乘一次,即是平方。
| 年 |
1 |
2 |
3 |
4 |
5 |
Total |
| 相差 |
0.64% |
1.44% |
0.04% |
7.84% |
4.84% |
14.8% |
將這些差額平方相加,再除以 5 ( 有 5 個數字,這做法可視為差額平方的平均數 ),14.8% / 5 = 2.96%,
這個數是方差( Variance )了。
由於差額平方了,因此需要把方差「開方」,來取得比較確實的數值。即是 1.72%。這就是標準差( Standard Deviation )。
這 5 年的回報率大部分位於 9.2% 正負 1.72% 的範圍內。
換個表達方式﹕這投資平均而言有9.2%的回報率,主要集中在介乎於7.48%至10.92%之間。
若標準差越大,如 6%,回報率的分佈廣闊,不太接近平均值,浪動很大,時高時低,風險謂之大也。
若標準差越細,如 0.1%,回報率的分佈窄狹,十分接近平均值,浪動很小,風險也細。
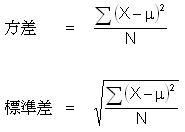
μ = 回報率的平均數。
X = 回報率
N = 回報率的數目。(有多少個回報率)
|

