一個消費者在某時間(t)，透過消費(C)而可以獲得到功用( Utility )，用 u(C_t) 表示。

人一生的所有功用，是把所有於不同時間的功用相加，而它受限於一生中消費了 多少(Lifetime Budget Constraint)，就是所有於不同時間的消費相加。

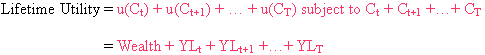
在有限的資源( 收入、財富 )，消費者會選擇可以獲得最大功用的消費。 最好的選擇是，每一個時間消費的 MU( Marginal Utility )相等，

如果不是相等，如MU在t 時比 t+1時高，即是於t 時消費可以獲得多一些功用，人便選擇於t 時多一些消費。
由於不知前景如何( Uncertainty )，也許你會知道 t 時的 MU，不過你未必知道 t+1 時的 MU。 因此，我們只能用 t 時的 MU來估計 t+1時的 MU。 把之前的式改一改，t+1 時的MU是 t 時MU的預期值，

雖然 MU Function 是不可以被觀察得到，不過，在這一個簡單的 case 中，要令之前的 Function相等， 只要轉一轉，以消費的角度看，

意思十分簡單，由於我們會選最大MU 的消費，如果消費相等，亦即是MU相等。

預計值也是不可以被觀察得到，不過到了七十年代時，Rational Expectation Theory(理性預期)的興起。
利用它的概念，下一個時期的消費，等於它的預期值，再加一個出乎意外的數值。

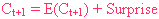
出乎意外的數值，按理性預期理論，它是一個隨機變數( Random Variable )。

把他們合併後，它變成一個 Random-Walk Model。

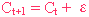
即是，人的消費是按上一段時期的消費而決定，再加上一個我們不知的因素，如突然地震，汽車意外等，而突然加或減我們的 消費。