一個小型的開放經濟體系由三個市場組成，「小」的意思是指它不能影響世界市場的價格，及世界的利率。 「開放」的意思是指它聯繫著世界的貨品及資本市場。

以下是這個 Model 的基本數式﹕

Goods Market
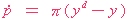	Philips Curve	( 1 )
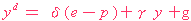	Aggregate Demand	( 2 )
Money Market
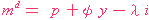	Money Demand	( 3 )
	Money Market Equilibrium	( 4 )
International Asset Market
	Asset Market Equilibrium	( 5 )
	Expectations Formation	( 6 )

這個 model 有兩條 curve，一是 IS，另一是 MS。 IS 是代表貨品市場，而MS 是代表貨幣及資產市場。

在物品市場處於均衡之下，需求等於供應 (y^d = y，π = 1 )。在這一個環境之下，價格水平處於穩定(沒有 通脹)，由( 1 ) 及( 2 ) 式，我們可得﹕

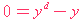IS :		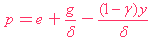( 7 )

貨品市場出現均衡，只有在某一個實質利率之下。而單是一個實質利率，已經可以由無限個不同的(名義)利率(e)及價格(p) 所組成。 所以組合可以用一條直線(IS)來表示，那條線的斜率是1。

貨幣市場與資產市場也是屬於「Monetary Sector」的成員，為了要得到均衡的條件，我們將兩個市場的均衡，合併起來。
把( 6 ) sub 入 ( 5 )，再將結果代入 ( 3 )中，再加上 ( 4 )﹕

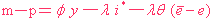MS :		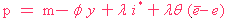( 8 )

在MS條的均衡上，出現了物價水平與匯率的反向關係。所有點在那均衡黠之外，是不可行的。 由於物品是包括在「Monetary Sector」中，加上利率及匯率是一些快速反應的variables，當有任何影響之時，都會 立即反應(令MS shift)，以保持Monetary Sector 中的永久均衡。
MS 的斜率是 －λθ。λ是預期匯率會走回均衡點的速度﹔θ是貨幣需求的利率(半)彈性。

我們首先找出一個外生(Exogenous)因素，如何影響匯率。

在( 8 )中，將e ＝ e，得出

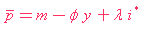( 9 )

把( 9 ) 代入( 7 )，

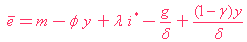			( 10 )

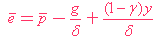在長期中，PPP(Purchasing-Power Parity)及QTM(Quantity Theory of Money)成立，

長期的實質匯率是﹕

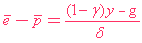( 11 )

可見，實質匯率亦是由Supply-Side及財政政策所影響。

現在考慮短期的波動。
把( 8 )解出 e，

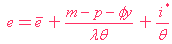( 12 )

要找出短期匯率的反應，我們只需把( 12 ) 用微分，d 一次。保持著物價是一個常數，貨幣供應的增加，影響匯率的效果﹕

在短期，在價格有反應之前，匯率的升幅比貨幣供應的升幅要大，並超越在長期時均衡狀態。匯率於是被過份提升(Overshoot)。