 Solow Condition 〔Lv 7〕 Solow Condition 〔Lv 7〕
Solow (1979) 提出他的論點,目的是找出其他令工資趨勢彊硬( Wage Stickiness )的其他原因。
建立 Solow Condition 之前,有一些工具需要用上﹕
A) 公司的盈利函數( Firm's Profit Function )(這裡的profit 是用一般的商用概念)
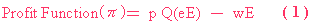
Q(eE) 是指生產數量 這裡的Q(eE)是解為「Q 是由 e 及 E 影響」
,不是Q 乘以(eE) 。
e 是指 Effort (可視為勞工的努力程度),e = e (w) ,
Effort is a function of wage (努力的多少由工資決定)。
p 是產品價格,在這裡假設了是在完全競爭市場,因此 p 是固定( constant )。
這裡亦假設了生產函數( Production Function )是簡單的把 Effort 乘以已顧用勞工的數量( E ,Employment)
。意思即是,如果勞工們努力多一倍,請一半人已經可以維持之前的生產量了。這只是一個假設,而且未必而事
實相符,只是一個大約準確的估值。因此原來Solow的版本是沒有假設這一個「相乘」的生產函數,不過他表示如果
要得出 optimal wage 是與產出無關的結果,生產函數是必須要這個模樣。
B) 用第一階微分(即是「d」一次那條profit function),求出 E 及 w 的最佳值﹕
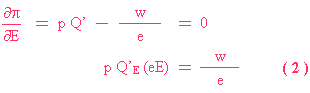
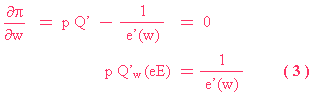
( 2 ) 是第一個條件,找出最佳水平的勞工投入量( Optimal Employed )。
( 3 ) 是第二個條件,找出最佳水平的工資( Optimal Wage )。
在此要介紹一個工具,名為「Wage - Effort Function」,它表示工資( w )與努力( e )的關係。而( 3 )式就正正是那條函數的數度。
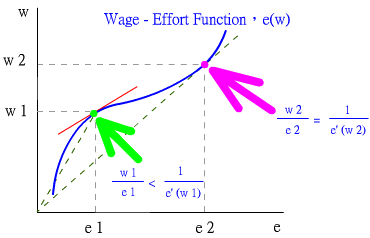
藍色的線是「Wage - Effort Function」,明顯地,人工與努力是成正比,即是人工越高,勞工工作越投入,付出更多努力。
公司是要找出定工資多少,從以獲得最佳的 effort。如果把人工定得偏低,如 w 1,相對得到的 effort 是 e 1。
在這一個情況之下,只要加小小人工,便可以換取較大量的effort。如果人工由 w 1 加至 w 2,effort 便會大幅上至 e 2。
而最佳的位置就是把人工定於上圖的紫色點。亦即是把之前 ( 3 ) 式等於 ( 2 ) 式。
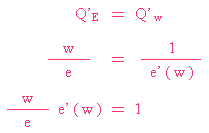
那個「一」的意思,正就是 Solow 的重點。它表示,如果在最佳工資的情況之下,工資改變某一個百分比,
努力同樣會改變那一個百分比。
結論是,人工不會輕易加減,以確保公司可以獲得所需的 effort,而只會透過勞工數目的加減來作成本的調節。
這一個 model 提供了一個解釋在經濟週期( Bussness Cycle) 中,工資的頑固性(Wage Rigidity)。亦建議出如果最佳
工資是比均衡工資高時,會有失業的情況。公司是不會隨便減低人工,以取得勞工超額供應之利。
一即以來,工資的頑固性大多是歸咎於勞工那方面,說勞工自私,不理公司死活等等........而Solow 的 Model 是由
公司那方面出法,公司亦希望工資是頑固性,令工資頑固性的觀點改變,其實是勞資相方也有推動的力量,令
工資出現頑固性。
|