E( b ) = E [ β + ( X' X )^-1 X' u ]
         = E( β ) + ( X' X )^-1 X' E( u )
         = E( β ) , E( u ) = 0
E( b ) = β

b 是沒有偏差( Unbiased )的 Estimator。

所謂 BEST ，其實是指它是否一個最有效率的 Estimator ，而有效率，主要是看它的 Variance ( 偏差 / 變化 ) 是否最細。

var( b ) = var [ β + ( X' X )^-1 X' u ]
           = ( X' X )^-1 X' var( u ) X ( X' X )^-1
           = σ²( X' X )^-1 X' X ( X' X )^-1
var( b ) = σ²( X' X )^-1

假設有另一個 Estimator 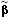，，它是一個任意( Arbitrary )的 Linear Estimator 。

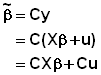
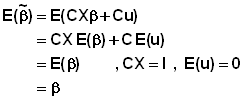
它是一個沒有偏差 ( Unbiased ) 的 Estimator 。

是時候入戲肉了，

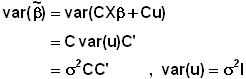
C = ( X' X )^-1 X' + D

CX = I   => ( X' X )^-1 X' X + DX = I
            => I + DX = I
            => DX = 0

CC' = [( X' X )^-1 X' + D]' [( X' X )^-1 X' + D]
      = ( X' X )^-1 X' X ( X' X )^-1 + DD'      , DX = 0 , X' D' = 0
CC' = ( X' X )^-1 + DD'

如果 DD' 是正數( Positive SemiDefinite ， PSD )，DD' ≧ 0 ，那麼

( X' X )^-1 + DD' ≧ ( X' X )^-1
CC' ≧ ( X' X )^-1
σ² CC' ≧ σ² ( X' X )^-1

由此推斷，透過 LS 找出來的 Estimator ，它的 Variance 是所有 Estimator 中最細，因而稱它為最好、最有效率( Best ) 。