你手上有兩組數據，分別近30年的GDP及私人消費，你希望找出它們的關係，這時你可以利用回歸模型。

X 是用作解釋 Y 的變數，用 Y= f(X) 表示。

在只有一個變數( X )去解釋 Y 的場合，稱為 Simple Regression Model，
如果有多個變數去解釋 Y，如有 X1、X2、X3，這稱為 Multiple Regression Model。

Linear 是指「直線」，Linear Regression Model 是指變數之間的關係，可以一條直線表示。
如果變數之間的關係，不是一條直線，如曲線，這稱為 Non-Linear Regression Model。

Simple Linear Regression 線性單方程回歸模型

Simple Linear Regression 又稱 2-Variables Linear Regression。

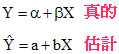
Y 及 X 均是變數( 我們手上的兩組數據 )，參數 α、β 是用來表示 Y 及 X 的關係。 因此，參數 α、β 是我們要找的東西。
可是真實 α、β的大小，只有上帝才知曉，我們是試圖去找出其近似值，而這些「估計」 出來的參數，用 a , b 表示。
而透過估計的參數來估計的 Y ( 我們想估計的變數 )，叫 Y Hat。( 在 Y 的頂部加一個 ^ )

真正的 Y 與估計的 Y，之間有一些差距，這差別稱為誤差( Error )。

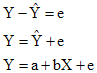
計算參數 a 或 b 的方程式，叫 Estimator。
而找出 Estimator 的方法有很多，最傳統的方法是「Ordinary Least Square Estimation( OLS ) 普通最小二乘法」。

以下是透過 OLS 找出的 Estimator。

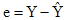
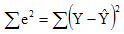
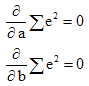
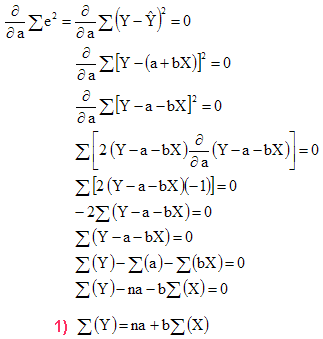
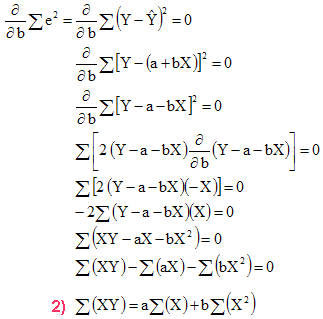
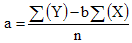
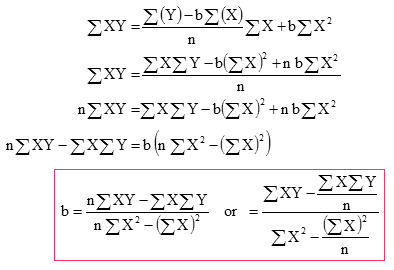
Ordinary Least Square Estimation( OLS ) 普通最小二乘法 「Square」指「Square Root」，即是將誤差自乘，由於誤差存在正值及負值，自乘便可以將負值消除。 OLS 就是透過「最小誤差」的概念來找出Estimator(如a及b)。 將 1) 變成， 再代入 2)， 使用相同的方法，找 a ，

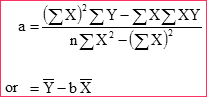
1.

1.