 Least Squares ( LS ) Principle
在同一個時間( t )，假設用一系列的因素( Variables ) X 去解釋 Y，得出以下一個模型( Model )。e 是解釋時出現的錯誤( Error )。
| Yt = b1 + b2 X2 t + ...
+ bk Xk t + e t
e t = Yt - b1 - b2 X2 t - ...
- bk Xk t |
b 是估計出來的參數( Parameters )，而我們的主角，就是要找出計算 b 的方程式。
Least Squares ( LS ) 是其中一個方式去找出 b 的方程式，事實上還有其他方法，不過 LS 是最基礎的。
LS 的做法是﹕在最少的 Σe t2 之下，b 的方程式。Least Squares 就是解為
「最少的 Σe t2」。
為了方便，假設 S = Σe t2 = Σ( Yt - b1 - b2 X2 t - ...
- bk Xk t ) 2
b2 也如是做一次。
把所有 b ( 由1至k ) 也與 S 微分一次，再等於 0 ，得出結果如下﹕
Σe t = 0
Σe t X2 t = 0
.
.
.
Σe t Xk t = 0
Σe t = 0 ，即是，
= Σ ( Yt - b1 - b2 X2 t - ... - bk Xk t ) = 0
= ΣYt - n b1 - b2 ΣX2 t - ... - bk ΣXk t = 0
n b1 + b2 ΣX2 t + ... + bk ΣXk t = ΣYt
Σe t X2 t = 0 ，即是，
= Σ ( Yt - b1 - b2 X2 t - ... - bk Xk t ) X2 t = 0
= ΣX2 tYt - b1ΣX2 t - b2 ΣX2 t2 - ... - bkΣX2 tXk t = 0
b1ΣX2 t + b2 ΣX2 t2 + ... + bkΣX2 tXk t = ΣX2 tYt
如此類推，便得出 k 條方程式。將之用矩陣( Matrix )表示﹕
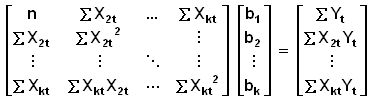
( X' X ) b = X' y
b = ( X' X )-1 X' y
|
|
